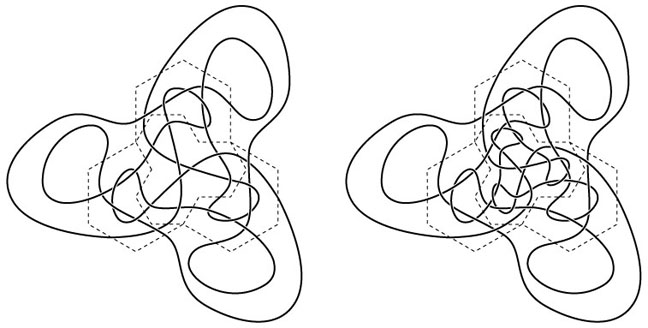
The starting curve is a dodecagon that can be formed by tracing around three regular hexagons fitted together. There is smaller dodecagon enclosed within it and touching it at three points. Each smaller iteration is scaled by the inverse of the square root of 3. This was actually derived from a fractal tiling, with the octagonal tile formed by the space between any two of the points where the dodecagons touch. The starting knot has 27 crossings, and 18 crossings are added with each iteration.
The starting knot and the first iteration, with the dodecagons shown in dotted lines:
After four iterations, with the outer strands modified for esthetic reasons:

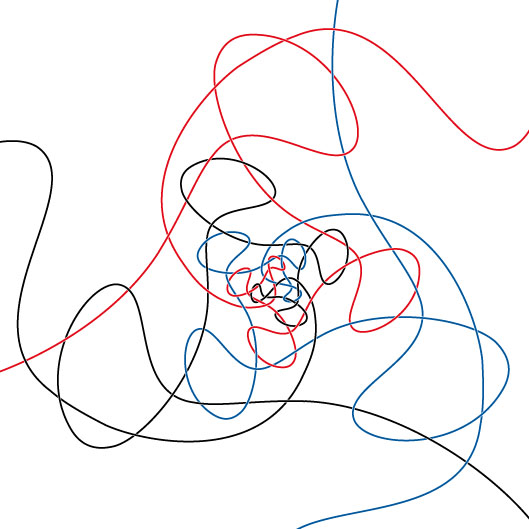
After four iterations, with three colors to better illustrate the path taken by the strand, and the outer portions of the loops cut off (the color would change as the strand transited each of the outer loops):