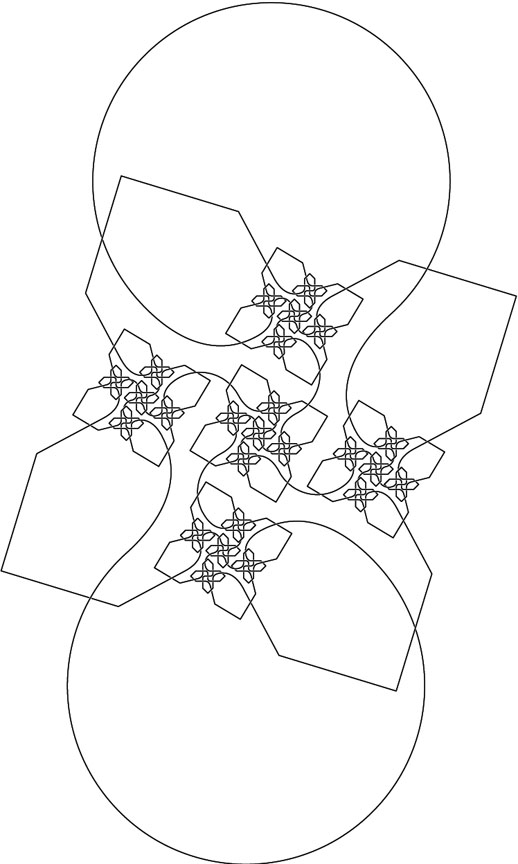
This knot employs a square as the starting curve, with five smaller squares embedded within it. This was derived from a fractal tiling created via dissection of a polyomino that leads to a scaling factor of the inverse of the square root of 17, and a rotation angle of around 14 degrees for each of the smaller squares. The starting knot has nine crossings, five of which are within the five smaller curves. It has two-fold rotational symmetry and would have four-fold symmetry if not for the exterior strands. Due to the rather severe scaling factor, iterating twice already leads to small features. The quintupling of features with successive iterations leads to a rapid increase in the number of crossings, from 9 for the starting knot to 49 for the first iteration to 249 for the second iteration. A third iteration would have 1,249 crossings! The increase in the number of crossings with each successive iteration is 40, 200, 1000, ...
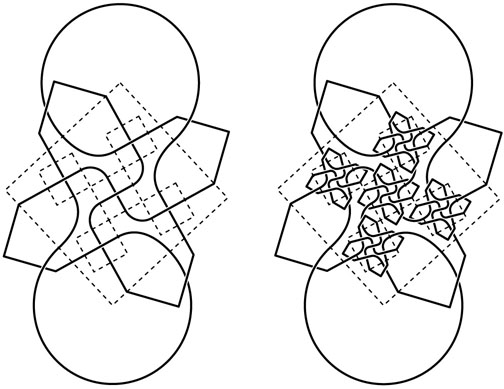
The starting knot and the first iteration, with the squares shown in dotted lines:
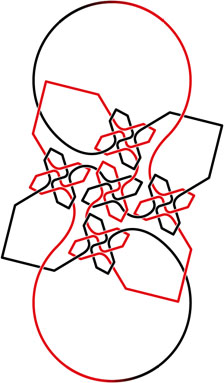
After one iteration, without the dashed lines, and with half the knot given a second color, to better show the path taken by the strand:
After two iterations: