
Introduction to Knots
Mathematical Knots
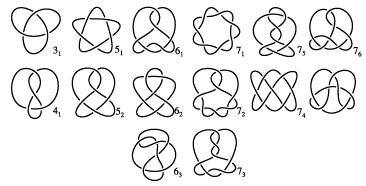
The utilitarian aspects of knots are familiar to everyone, starting with learning to tie your shoes as a child. Mathematicians are interested in knots as well. The mathematically-distinct knots have been studied and tabulated. The smallest number of crossings a knot can have is three, and there is only one possibility, known as the trefoil knot. There is only one possibility with four crossings as well, but two possibilities with five crossings, three with six crossings, and it grows rapidly after that. By definition, a mathematical knot consists of a single strand. An object with more than one strand is called a link. A portion of the knot table is shown below, where the first number specifies the number of crossings and the second enumerates distinct knots with that number of crossings.
Decorative Knots
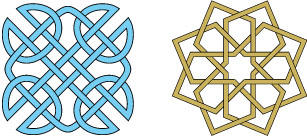
Decorative knotwork has played a role in many cultures from very early on. Applications range from textiles to architecture. Celtic and Islamic designs are particularly rich in the use of knot motifs. In the case of Islamic art, complex and sophisticated latticework define geometric shapes such as star polygons. These designs were widely used to decorate buildings like the Alhambra palace, in Granada, Spain, as well as mosques. Simple examples of Celtic (left) and Islamic (right) knot designs are shown below.
Click here to browse products related to knots.
Math + Art topics
mathartfun.com home
© 2000-2015 Tessellations



