Compendium of Fractal Tilings
by Robert Fathauer
(version 2.0 - last update July 2008)
General Remarks
Tilings and fractals are perhaps the two topics where art and mathematics come together most wonderfully. Despite this, no one seems previously to have thought very much about combining the two. This is what the Compendium of Fractal Tiling addresses, by cataloging distinct fractal tilings of the plane (two-dimensional Euclidean space). These fractal tilings are not proper tilings in two respects. First, they do not cover the infinite plane, and second, they contain singularities (see definition below). To distinguish them from proper tilings, they will be referred to f-tilings.
In order to make this task somewhat managable, I'm restricting it to tilings that are bounded, and for which the same simple algorithm can describe the relationship between any two successive generations of tiles within a given tiling. In addition, only f-tilings based on a single prototile are described here.
Almost of the f-tilings included here are edge to edge; those that are not will be so noted. Most, but not all, of them have fractal boundaries; f-tilings with fractal boundaries are in general of greater aesthetic appeal than those with non-fractal polygonal. Most of the prototiles are polygons with a finite number of edges, though a few examples are given of f-tilings with fractal tiles, which have an infinite number of edges. No attempt is made to include fractal tiles that tile in non-fractal manner. In addition, simple spiral tilings, in which the tiles get smaller and smaller as they approach a center point, are not included here. While such tilings are technically fractal, their construction is relatively trivial.
The Compendium is a living document, residing on the World Wide Web. The initial version (1.0) was uploaded in June of 2000. My initial intention was to update it frequently, but I didn't manage to do that, in spite of the fact that I discovered a great variety of new f-tilings after that date. A major revision (version 2.0) was uploaded in July of 2008.
This work is intended for the non-specialist and is largely oriented toward the aesthetic appeal of tilings. It is not couched in formal and rigorous mathematical language. For this reason, the serious mathematician may find it a bit unsatisfactory, but I think all of us will be able to enjoy these fascinating constructions.
My fascination (bordering on obsession at times) with this topic stems from my interest in the art of M. C. Escher, who touched on tilings of this sort. His best known prints with diminishing motifs are based on hyperbolic (non-Euclidean) geometry, however, which is outside the scope of this work. For some of the f-tilings in the Compendium, I have designed an Escher-like, recognizable motif. In a few cases, such motifs have been designed by others as well. These are shown, where possible, along with the geometric f-tiling.
Most of the f-tilings contained in the Compendium were, to the best of my knowledge, discovered by me. I say "discovered" rather than "invented", because they already exist in the mathematical fabric of our universe (so to speak), and are just waiting to be uncovered. Any f-tilings discovered by others will be noted as such.
The f-tilings are classified and identified (for the most part unambiguously) by a descriptor, as described below. They are in organized three different ways - by the number of edges possessed by the prototile, by the rotatonal symmetry of the overall f-tiling, and by a polygon or polyform from which the prototile may be derived by dissection. The table of contents at left can be used to access these different listings, each of which contains subcategories. Many of the f-tilings can be accessed from more than one listing.
Definitions
A fractal is an object that possesses self similarity on different scales, with these scales being related mathematically. E.g., if one chooses a particular region and zooms in 5x, it looks the same. If one zooms in another 5x, it looks the same again, etc. There are numerous web sites dedicated to fractals for the reader interested in learning more about them.
A tiling is a collection of shapes (tiles) that fit together to cover the plane, without overlapping or leaving gaps.
A fractal tiling or f-tiling is a tiling in which the arrangement of tiles is fractal.
A prototile is a tile to which all other tiles in the tiling are similar; i.e., of the same shape, though not necessarily the same size. At this time, the Compendium is restricted to tilings that have a single prototile.
An edge of a (polygonal, or many sided) tile is a single straight line segment.
A vertex of a tiling is a point at which three or more tiles meet. A corner of a tile is a point at which two edges meet.
An edge-to-edge tiling is one in which all edges of any two tiles that meet do so along the entire lengths of the two edges. In an edge-to-edge tiling, the corners of the tiles correspond to the vertices of the tiling.
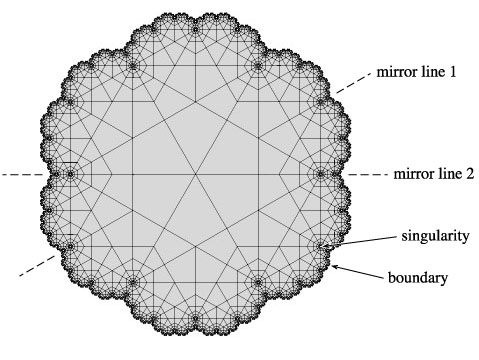
A bounded f-tiling is one that contains an infinite number of tiles within a finite area. The boundary of an f-tiling is the collection of points within which all of the tiles are contained.
A singularity is a point where tiles become infinitesimally small. I.e., any finite area containing a singularity will contain an infinite number of tiles.
Construction of the Fractal Tilings
The general method used to construct most of the f-tilings is described here. This does not apply to those f-tilings with fractal prototiles. An illustrative example is provided in figures.
1. A prototile is chosen that possesses edges of two lengths, denoted "long" and "short". Note that most prototiles one might choose will not fit together without overlapping or leaving gaps. The challenge is to discover those that will.
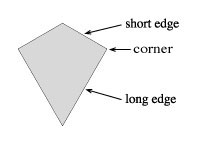
2. Two or more prototiles (the "first generation") are arranged about a point (the eventual center of the f-tiling) such that a group with rotational symmetry is formed, and all long edges are paired up.
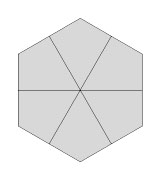
3. Second generation tiles are created by scaling first generation tiles by the ratio of the short to long edges. These are arranged around preceding generations according to a simple set of rules.
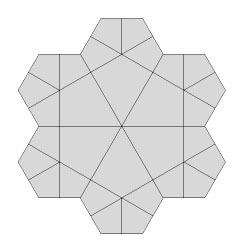
4. Additional generations are created and arranged around preceding generations according to the same set of rules. This process is carried out an infinite number of times in theory. For the figures in the Encyclopedia, a sufficiently large number of generations has been created to illustrate the general form of the infinite f-tiling. The resultant f-tiling is often very difficult to predict, and can be quite unexpected, from which derives the pleasure in discovering these f-tiling.
Classification of the Fractal Tilings
A classification system is used to identify and describe the f-tilings. The classification descriptor is of the form (p#, r#, g#, s#, m#). The # sign denotes a number, integer for all of the descriptors but s. The different descriptors are as follows:
"p" gives the number of edges for the polygonal prototile. For example, a quadrilateral prototile is designated "p4".
"r" gives the rotational symmetry of the f-tiling. For example, a 5-fold rotationally symmetric f-tiling is denoted "r5". This means that the f-tiling, if rotated by 1/5th of a full revolution about its center, is unchanged.
"g" gives the ratio of second generation tiles to first generation tiles. For example, if 24 second generation tiles fit around 6 first generation tiles, this is denoted "g4".
"s" gives the scaling factor from one generation to the next smaller generation, which is the same as the ratio of the short to long edges of the prototile. This factor is rounded off to three decimals.
"m" gives the number distinct lines of mirror symmetry. The f-tiling will remain unchanged if it is reflected about a line of mirror symmetry.
By way of example, the f-tiling shown above is classified as (p4, r6, g4, s.577, m2).
Perforated Fractal Tilings, Coloring of the Fractal Tilings, and Digital Art
For the purpose of making f-tilings that are more interesting and aesthetically pleasing, a few of the f-tilings have been modified by a process I call "perforation". This refers to removal of the largest generation or two of tiles, following by completing the largest remaining generation of tiles so that all long edges are matched up, and then building in with smaller generation tiles. In some cases, multiple perforation steps have been carried out. Perforated f-tilings will be noted as such.
The f-tilings have been colored to make the construction more clear and also to add to their aesthetic appeal. In most cases, each generation of tiles is given a different color.
In addition, some of the tilings have been rendered in more fanciful or dramatic fashion to create digital artworks. This might consist of coloring the tiles and adding a backdrop, or in some cases a more dramatic alteration. Such figures will be described as digital artworks based on the particular f-tiling.
Copyright and Reproduction of the Figures
All figures in the Compendium are copyrighted by Robert Fathauer. Please request permission to reproduce any of the figures for any purpose.
Go to Fractal Tiling Compendium Home
Webmaster: Robert Fathauer; rob@tessellations.com