Magic-Numbered d20 and d30
The world's first numerically-balanced 20-sided and 30-sided dice!
In order for dice to be as fair as possible, physical and numerical balancing are both important. Read below to learn more about numerical balancing of dice and how our d20 and d30 are unique. The Dice Lab d20 and d30 are offered in blue, red, green, white, and black. All our offerings are available online at The Dice Shop at Mathartfun.com.
Physical balancing of dice requires use of isohedral polyhedra. The polyhedra traditionally used for the d20 and d30 are such polyhedra. Perfect physical balancing is still not possible, though, due to physical differences in numbers, small inaccuracies in molds, additional inaccuracies introduced during tumbling, and density variations due to defects like voids. In addition, it's possible to affect the roll of dice to a degree by carefully controlling the manner in which they're tossed. For these reasons, dice are more fair if they are numerically-balanced as well. For example, a void inside a die near a vertex (a point where three or more faces come together) will cause that vertex to preferentially face up when the die is tossed. The effect of such defects can be minimized by arranging the numbers such that the sum of the faces meeting at each vertex is the same.
Dice are traditionally numbered such that the largest number is located opposite the smallest, next largest opposite next smallest, etc. For a d20, 20 is opposite 1, 19 opposite 2, 18 opposite 3, etc. The average value per face is half of 21, 10.5. If a die is unintentionally oblate (slightly flattened on opposing sides), the flatter regions are more likely to turn up when the die is tossed. If these two opposite numbers were 19 and 20 for example, then the die would on average roll high, since these two numbers would come up too often. Having the two numbers add to 21 avoids any such bias in the average number rolled. For this reason, the opposite-side numbering convention improves fairness. Equally important in our opinion is balancing of the vertex sums.
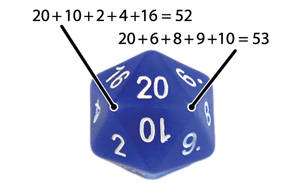
In the standard d20 numbering, small and large numbers are distributed more-or-less evenly over the die, with the following vertex sums: 39, 47, 49, 51, 52, 52, 53, 53, 54, 56, 58, and 66. Using computer search techniques, we've managed to find a numbering with ideally-balanced vertex sums while retaining the opposite-side numbering convention: 52, 52, 52, 52, 52, 52, 53, 53, 53, 53, 53, and 53. In analogy to Magic Squares, in which each row, column, and diagonal sum to the same number, we call such a numbering of a die a "magic" numbering. The d20 is the only one of the standard polyhedral dice (d4, d6, d8, d10, d12, and d20) that allows a magic numbering.
A d30 has 32 vertices, of two types; 20 where three faces meet and 12 where five faces meet. Since the average face value is 15.5, an ideal numerical balancing would have ten vertices summing to 46, ten summing to 47, six summing to 77, and six summing to 78. We found a dozen ideal numberings based on these criteria.
As icing on the cake, in our d20 the sum of the three faces adjacent to a face is also ideal, with sums of 31 for ten faces and 32 for the other ten. For the d30, ideal face sums are not possible, but we chose a vertex-sum solution that was nearly ideal as regards a face criterion. The numberings of The Dice Lab's d20 and d30 were worked out by Bob Bosch, a Professor of Mathematics at Oberlin College. Our d20 measures 22 mm face-to-face, making it slightly larger and heavier than most d20s, which are typically 19-20 mm. Our d30 measures 27 mm face-to-face
Video about the numerically-balanced d20:
About us
 Dealer information
Dealer information
 Where to Buy
Where to Buy
 Press Room
Press Room
 Contact us
Contact us
 Home page
Home page
© 2015 Tessellations