Dice Design at The Dice Lab
The Dice Lab's unique designs are created by the two-person team of Robert Fathauer and Henry Segerman. Robert has a background in experimental physics, having worked as a researcher at the Jet Propulsion Laboratory. He is also a "semi-professional" artist, having shown his work in numerous exhibits and done commission work for several clients. His mathematical art can be seen here.
Henry Segerman is a math professor at Oklahoma State University specializing in geometry and topology. He is well known for his innovative mathematical art and models created using computer design and 3-D printing. Henry's work can be seen here.
A well-designed die is both fair and esthetically pleasing. When tossed, a fair die yields its various numbers or symbols with equal probability, regardless of details of the surface or the toss. The shapes of dice are based on polyhedra, solids whose faces are polygons. To ensure fairness, each face of the polyhedron should have an identical relationship to the other faces. Unfortunately, nature only allows this for certain numbers. Furthermore, some of the allowed polyhedra are better suited to use as dice than others, and some just look better. For example, a regular dodecahedron, commonly used for the d12, is a beautiful solid that tumbles well. In contrast, the best option for a fair d10 has two sets of five faces arranged on either side of an "equatorial" band, a design that neither looks very good nor tumbles well.
Design notes on each of our unique dice follow. Considerable thought went into the numbering of the dice. The starting point was locating the largest number opposite the smallest number (on opposing faces), the next largest opposite the next smallest, etc. This convention is widely followed in dice design. The next priority was to distribute the numbers as uniformly as possible. That was accomplished by balancing the sums of the numbers on each group of faces surrounding a vertex. For the d12, d24, and d60, there are two or three different types of groups. We prioritized these by first trying to balance the groups that catch the eye the most (by approximately forming a regular polygon). Note that the average numerical value per face for an n-sided die is (n + 1)/2.
Our d4 is based on the truncated tetrahedron. The standard d4 is a regular tetrahedron, and the truncated tetrahedron offers some advantages: 1) The numbers can face straight up; 2) This shape rolls and tumbles better; and 3) It's easier to pick up. A drawback to the truncated tetrahedron is the fact that it can land on a small triangular face, which we've found happens about 3% of the time. There is only one distinct choice for distributing the numbers on the four triangular faces. The use of this polyhedron for a die was previously described by Joseph Fjelstad.
Our d8 is based on the truncated octahedron. This design was chosen both for the fact that it is a space-filling polyhedron and because truncation creates a polyhedron that is more nearly spherical. This means it rolls and tumbles better than a regular octahedron. A drawback to the truncated octahedron is the fact that it can land on a square face, which we've found happens about 2% of the time. Due to the small number of faces, perfectly balancing the sums over the six groups of four faces isn't possible if the numbering convention of 1 opposite 8, 2 opposite 7, etc. is followed. However, our d8 has the most nearly balanced sums possible: 14, 16, 18, 18, 20, and 22, unlike other d8s on the market. The sums for the numbering used by the leading dice manufacturers are 10, 16, 18, 18, 20, and 26.
Our d12 is based on the rhombic dodecahedron. While a regular dodecahedron makes for a good design, the rhombic version is a nice complement to it. This polyhedron is also a space filler and is closely related to both the cube and regular octahedron.
Our d24 is based on the deltoidal icositetrahedron. The d24 dice currently on the market are tetrakis hexahedra, in which each face of a cube is replaced by a square pyramid. The faces of this polyhedron are relatively wide and short triangles (not ideal for numbering), and there are more esthetically-appealing icositetrahedra. The deltoidal version is probably the most attractive one that possesses parallel opposing faces. It has eight groups of three faces, six groups of four faces meeting along long edges, and twelve groups of four faces with two long and two short edges meeting. Due to the large number of possibilities for distributing the numbers, Henry wrote code to determine the optimum numbering. He found 86 solutions which perfectly balance the sums for the first two types of groups. Of these, the best balancing of the other twelve quadruples has sums ranging from 44 to 56 (4 x 12.5 = 50).
Our d48 is based on the disdyakis dodecahedron. This is the world's first injection-molded d48. Bob Bosch, a mathematician at Oberlin College, found a numbering that perfectly balances the sums for all of the vertices. This die is in some ways a companion to our d120. The disdyakis dodecahedron is formed from the rhombic dodecahedron by placing a four-sided pyramid on each rhombus, while the disdyakis triacontahedron is formed from the rhombic triacontahedron in the same manner. Both dice present a challenge in fitting the numbers into narrow triangular faces.
Our d60 is based on the deltoidal hexecontahedron. This is the world's first injection-molded d60. There are so many choices for numbering the faces that it wasn't practical to compute all of them. A solution was found that perfectly balances the sums for all twelve groups of five faces and all twenty groups of three faces. The polyhedron also has thirty groups of four faces, but these don't jump out to the eye as readily, as they again have two short and two long edges meeting in a group. The sums for these aren't particularly well balanced.
Our d120 is based on the disdyakis triacontahedron. This is the world's first injection-molded d120. 120 is the maximum number of faces possible in an isohedron, excepting dipyramids and trapezohedra, which aren't workable solutions for physical dice with more than about 50 faces. Even requiring the pairing of opposing faces in conventional fashion, with 1 opposite 120, 2 opposite 119, etc, the number of possible numberings is astronomical. After weeks of searching with sophisticated techniques, Bob Bosch, a mathematician at Oberlin College, found a solution that perfectly balances the sums for all of the vertices. Twelve vertices have ten faces meeting at them, twenty have six faces, and thirty have four faces. In order to allow adequate space for numbers and firm settling on a face, our d120 is unusually large for a die, with a diameter of 2" (50 mm), and a weight of 0.2 lb. (95 gm.).
Skew Dice
Skew d12 Dice
The d2/3/4 MultiDie is based on the rhombic dodecahedron. We modified the polyhedron by rounding down the eight vertices at which three faces meet. These eight locations were used for the d4 numbers 1-4 (once each, inset in triangles) and the d2 numbers 1 and 2 (twice each, inset in circles). The d3 numbers 1-3 were placed in the centers of the twelve faces, with each number appearing four times. The effect of all this is to show one up-facing number of each type for a given roll. Not only does this design provide three dice in one, but it tumbles nicely. Designs for a d3 or d4 with only three or four sides don't tumble well due to the large angles between faces. For selecting between two choices, rolling a die is easier and more satisfying than flipping a coin. A triangle was used around the d4 numbers because standard tetrahedral four-sided dice have triangular faces. A circle was used around the d2 numbers because flipping a coin is the traditional way of randomly selecting between two choices. Since all three d3 numbers appear for any d4 or d2 value, a single roll can be considered independent fair rolls of both the d3 and either the d2 or d4. The idea for a three-in-one d2/3/4 die is due to Jimmy Kerl, who participated in the design process.
Our numerically-balanced d20 is based on the icosahedron, one of the Platonic Solids. This polyhedron is widely used in sets of standard polyhedral dice. In contrast to other d20s, though, ours is magic numbered. This means the sums of the faces meeting at each vertex are equal (or in this case, half are 52 and half 53, since the average is 52.5) while retaining the opposite-face numbering convention in which 1 is opposite 20, 2 opposite 19, etc. Such a numbering is ideal from the standpoint of compensating for any physical imbalance or defects that could bias the roll of dice. In addition, our d20 is slightly larger than most d20s on the market.
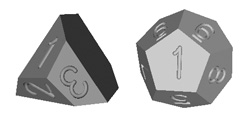Rolling and summing this pair of dice yields the same 36 possible results as a pair of standard six-sided dice. Robert found this numbering in analogy to the numbering of the d6 pair designed by Col. George Sicherman. Sicherman dice are six-sided dice marked with different integers from the standard d6 dice, but giving the same probability distribution for the pair. They were discovered as a solution to an algebraic equation, and the d3/d12 pair can be found in similar fashion.
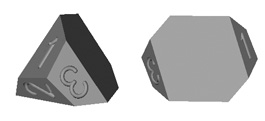The only way to design fair dice with an odd number of sides is to use some variation of a prism that can't land on the ends. One way to do this is to round the ends, but that makes numbering difficult. Our solution is to facet the ends and make the large faces hexagonal. The subtlety that really makes this a great design in our opinion is angling the end faces and skewing the hexagons. This allows for relatively large end faces without an overly-long middle section. It's impossible for these dice to settle on an end face, as the center of gravity is off the face, causing it to fall onto a large blank face.
Our OptiDice d10s measure 18 mm face to face. This compares to 16 mm for typical d10s, meaning the Dice Lab version weighs about 40% more. The use of our copyrighted hexagon-based numbers means that the same amount of material is removed for the numbers on each face. In addition, the dice have the most balanced numbering allowed by the geometry. Most d10s have all the odd numbers on one half and all the even numbers on the other half. This leads to a higher average roll for one half, which could allow the toss to be cheated to gain an advantage and would cause a more unfair result if a die had a void or other defect that led to landing on one half being preferred. For the groups of five faces surrounding the polar vertices, the sum for typical d10s is 20 and 25, while the Dice Lab d10 sums are 22 and 23. For the other ten vertices, a Chessex d10 has sums of 10, 11, 11, 11, 12, 15, 16, 16, 16, and 17. The Dice Lab d10, in comparison, has sums of 11, 12, 13, 13, 13, 14, 14, 14, 15, and 16.
Dealer information
Where to Buy
Press Room
Contact us
Home page