Introduction

These web pages describe and show a number of "fractal" (strictly speaking, iterated) knots, as well as related animations and artworks. A widely-applicable method for iterating knots, first presented at the Bridges Conference in 2007, is described in this introduction. This method relies on substitution of portions of a knot with smaller copies of the entire knot. A starting knot is first arranged as a patch of tiles that contains individual tiles similar in shape to the overall patch. Iterative substitution leads to the creation of complex knots that are often esthetically pleasing, particularly for knots possessing a high degree of symmetry. The iteration process is designed to allow repetition ad infinitum; i.e., an infinite number of iterations leads to a unicursal fractal that is, therefore, a (wild) knot. This method is described in detail below.

A second method for iterating knots was presented at the Bridges Conference in 2009. This method utilizes a starting curve in which smaller copies of the curve are embedded. Points along the curves are connected by strands to form a knot, which is iterated by replacing the contents of the smaller curves with those of the larger curve. In contrast to the first method, based on locating the strands along the edges of tiles and the crossings at vertices, the new method is based on placing crossings within the curves. The two methods allows the construction of esthetically pleasing knots in different situations and thus complement one another. The second method is described in a series of slides, the first of which can be seen by clicking here. The papers written for the two Bridges Conference proceedings are available as pdf files on the References page.

Fractal Knots Created by Iterative Substitution

Fractals and knots are areas of mathematics with considerable visual appeal, but to date there have been very few reports on combining the two. Fractals are constructed by iteratively performing a series of steps, so the natural way to combine the two is to make those steps some sort of knot construction process. A couple of examples of iterated knots were presented by Carlo Séquin in 2005 [1]. Paul Gailiunas presented an iterated knot at the Bridges conference in 2006 [2] that was based on the Sierpinski gasket. While these constructions were only iterated a few times, they in principle could have been iterated ad infinitum. Also at Bridges 2006, Robert Fathauer exhibited fractal link designs [3]. These were created by decorating fractal tilings with knot-like graphics, but consisted of an infinite number of strands, while the examples of Séquin and Galiunas were true knots (consisting of a single strand, or "unicursal").

A technique is presented here for generating fractal knots that is readily applicable to a wide variety of knots. Careful choice and arrangement of the starting knot can lead to results with considerable visual appeal. In many cases, the resulting fractal is unicursal, and therefore a knot. Since these fractals contain an infinite number of crossings, they are not proper or "tame" knots, but "wild" knots. In the figure captions, the starting knots are described by both their Alexander and Briggs and Conway notations [4].

Description of the Method

The method can be described as follows. An example is provided in Figure 1.
1. Select a particular projection of a starting knot (Figure 1a) and rearrange it from the canonical drawing to a more self-similar one, in which some of the gaps in the knot are similar in shape to the overall knot (Figure 1b). This rearrangement, the "starting self-similar knot," is carefully chosen to be analogous to a patch of tiles (Figure 1c), the edges of which are traced out in non-overlapping (excluding crossings at points) unicursal fashion. This patch of tiles has the following properties.

The patch has an overall shape that occurs one or more times in individual tiles in the patch (the "substitutional tiles," shaded in Figure 1c). In the examples presented here, the number of substitutional tiles is two or more, as a single tile results in a rather trivial example of a fractal knot.
The valence of each vertex in the patch is four. While larger even numbers are allowed, they lead to the crossing of more than two strands at a single point, which is visually ambiguous and thus undesirable.
Crossings do not occur at points on the boundary of the patch that will coincide with existing crossing points when the knot is scaled down and substituted, as this would result in points at which more than two strands cross. In addition, the crossings should alternate in over/under fashion.

2. Replace the portions of the current knot corresponding to the substitutional tiles with scaled-down copies of the starting self-similar knot (Figure 1d). The scaled-down knots should be rotated and/or reflected as necessary.
3. At points where the scaled-down knot meets the original knot, join the strands so that the alternating over/under weave of the knot is maintained. This new and more complex knot is the "current iterated knot."
4. For the next iteration, use the current iterated knot as the starting point and repeat steps 2 and 3. Figure 1e shows the resulting knot after two iterations.

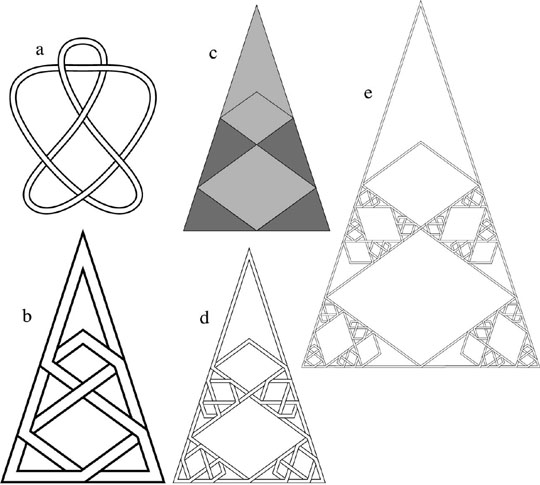
Figure 1: An illustration of the process of iterating a particular projection of the knot 6₂ 312. (a) The canonical drawing of the knot. (b) A more self-similar drawing. (c) Representing the knot of Figure b as a patch of tiles, four of which (shaded) are similar in shape to the patch. (d) The knot after one iteration guided by Figure c. (e) The knot after two iterations.

The construction generated by the above process may or may not be unicursal. This can be determined by tracing the first and second iterations. If they are unicursal, consistent application of the iteration rules will guarantee that the constructions resulting from additional iterations will also be unicursal. In many cases the iteration process results in two or more separate strands. In such cases, a different choice of path along the tile edges or a different tiling patch may result in a unicursal construction.

Further Examples

Knots with uniform strand width. In this section, additional examples of iterated knots constructed using the method described above are presented. The strand width is kept constant within a given iteration and is scaled along with the knot when iterating.

In Figure 2, the goal in designing the iterated knot was to minimize the shrinkage between successive generations, so that a large number of generations could be seen at once. For this reason, a simple knot and a patch of tiles with only two smaller copies were selected. The irregular shape of the tiles results from adjusting the starting self-similar knot to allow a minimal shrinkage, while being careful to allow space between all of the strands. The scaling factor for this iterated knot between successive generations is 1 / √ 3 (approx. 58%). With this knot, it was necessary to reflect the substituted portions to maintain an over-under weave.

In Figures 3 and 4, more stylized examples are shown, where the iterated knots evoke Islamic lattice designs. In Figure 3, the number of knottings quintuples between successive generations and the scaling factor between successive generations is 1/3. In Figure 4, the number of knottings quadruples between successive generations and the scaling factor between successive generations is again 1/3. In both these examples, the starting patch of tiles is not quite a regular polygon, but has some triangular dents at the boundaries. After iterating, this leads to individual "tiles" or holes in the design that are fractal. This is in contrast to the knots in Figures 1 and 2, in which the holes remain simple polygons.

Note that perceptually there is a reversal of positive and negative space between the drawings of tile patches and knots. I.e., tiles are perceived as positive space, with the lines between them (which are infinitesimally narrow in a mathematical tiling, but necessarily possess finite width in a drawing) perceived as negative space. In the knot drawings, the strands are perceived as positive space, and the gaps between them as negative space.

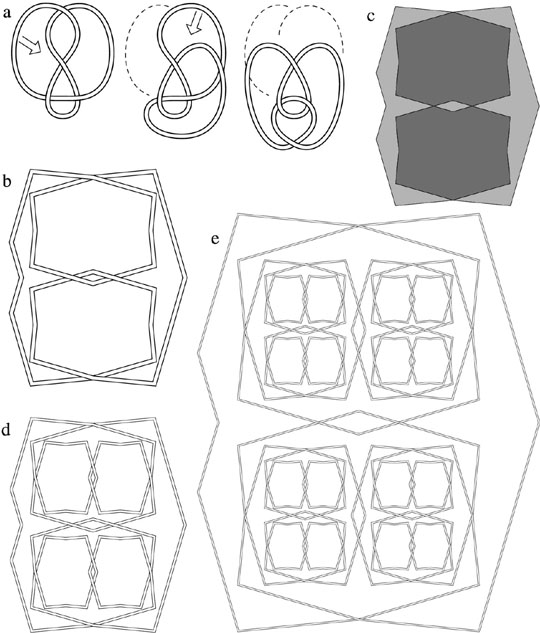
Figure 2: Iterating a particular projection of the knot 4₁ 22. (a) The canonical drawing of the knot is shown at left, along with a series of Reidemeister moves that reconfigure the knot. (b) A more self-similar drawing of the reconfigured knot. (c) Representing the knot of Figure b as a patch of tiles, two of which are similar in shape to the patch. (d) The knot after one iteration guided by Figure c. (e) The knot after three iterations.

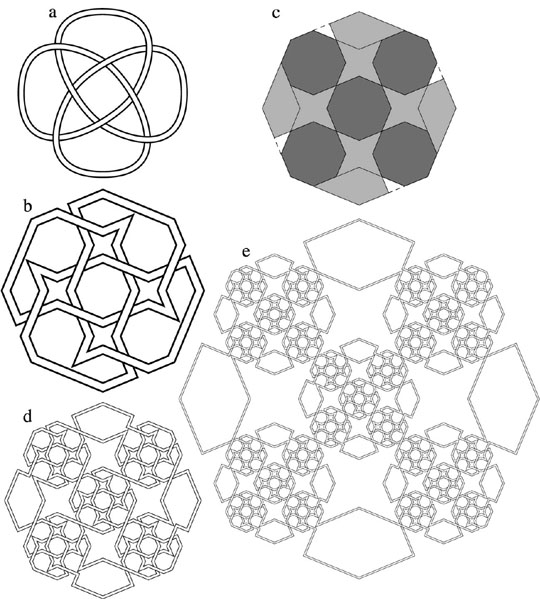
Figure 3: Iterating a particular projection of the knot 8₁₈ 8*. (a) The canonical drawing of the knot. (b) A more self-similar drawing of the reconfigured knot. (c) Representing the knot of Figure b as a patch of tiles, four of which are similar in shape to the patch. (d) The knot after one iteration guided by Figure c. (e) The knot after two iterations.

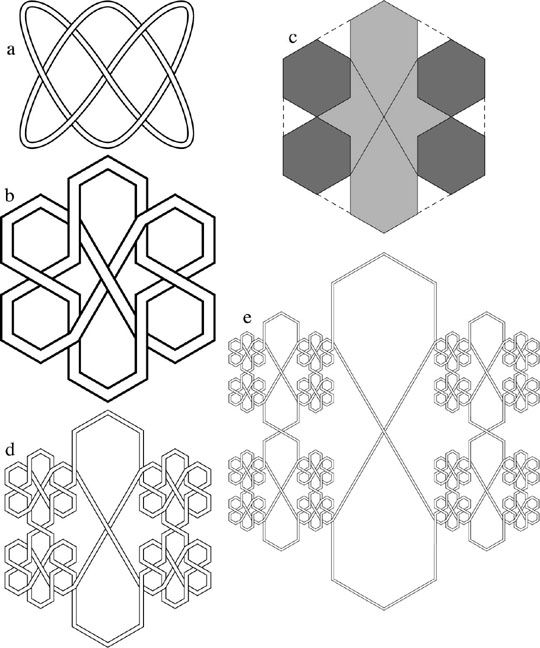
Figure 4: Iterating a particular projection of the knot 7₄ 313. (a) The canonical drawing of the knot. (b) A more self-similar drawing of the reconfigured knot. (c) Representing the knot of Figure b as a patch of tiles, four of which are similar in shape to the patch. (d) The knot after one iteration guided by Figure c. (e) The knot after two iterations.

Knots with visual self-similarity at different scales. Iterating a knot using the method described above ad infinitum results in a fractal knot. However, visually such a knot would not form a very satisfactory fractal. Even if the strands were given finite width in the starting knot, they would become infinitesimally small after an infinite number of iterations, so that nothing would be seen at any finite magnification.

This problem can be circumvented by maintaining the original strand width in the portions of the iterated knot that remain unchanged. Figures 5a-c illustrate this process for the knot of Figure 4. Joining the thicker to thinner strands requires a telescoping of the strand width. After a large number of iterations, only these thicker portions would remain visible, giving the knot the appearance shown in Figure 5c. In this example, every strand segment necks down to infinitesimally narrow width at the points where they join the next generation.

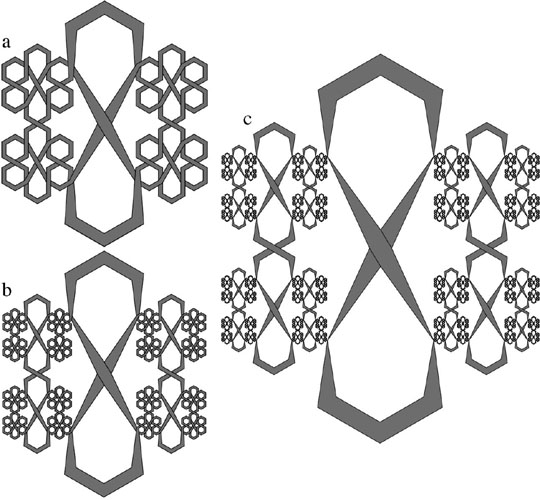
Figure 5: A rendering of the knot shown in Figure 4 that allows features to be seen at a finite magnification after many iterations. (a) After the first iteration. (b) After the second iteration. (c) Approximate appearance after an infinite number of iterations.

Another example is given in Figure 6, where the simplest non-trivial knot, the trefoil knot, is rearranged to form a circular starting self-similar knot. With each iteration, two copies of the knot are scaled by a factor of 1/2 and rotated 90 ° . In order to obtain visual self-similarity, the strand width is varied continuously so that the strands of the smaller knots match those of the larger knots. In this example, the strand segments decrease to infinitesimally narrow width where they join the next generation, but only by a factor of 1/2.

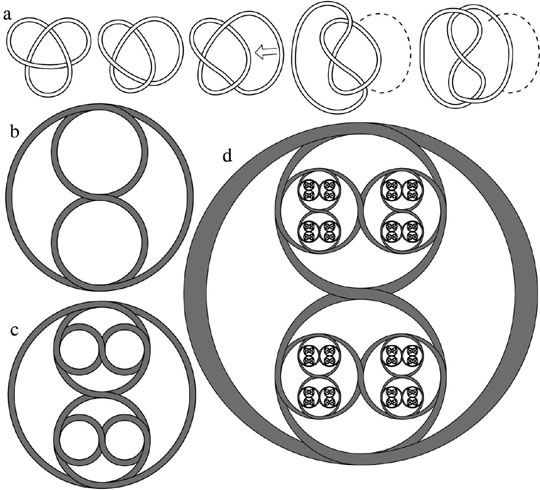Figure 6: (a) A rearrangement of the trefoil knot for iterating. (b) The starting self-similar knot. (c) After the first iteration. (d) Approximate appearance after an infinite number of iterations, where the strand width is varied to scale with the knot.

In summary, this page describes a method for iterating knots that is based on substituting a portion of the starting knot with a scaled-down copy of the full knot. In the limit of an infinite number of iterations, the resulting construction is fractal and in many cases unicursal, and therefore a knot. The key to obtaining an esthetically-pleasing iterated knot is the arrangement of the starting knot in a more self-similar and sometimes more symmetric manner.

References

[1] Carlo Séquin. Tangled Knots, presented at the Art+Math=X conference in Boulder, Colorado, June, 2005. Presentation available at http://www.cs.berkeley.edu/~sequin/.
[2] Paul Gailiunas, Knot Designs from Snowflake Curves, in Proceedings of the Bridges 2006 Conference, edited by Reza Sarhangi and John Sharp, pp. 581-584, 2006.
[3] Robert Fathauer, Fractal Tilings Based on Dissections of Polyominoes, in Proceedings of the Bridges 2006 Conference, edited by Reza Sarhangi and John Sharp, pp. 393-300, 2006. Also artworks included in the conference art exhibit; available at http://www.bridgesmathart.org/art-exhibits/bridges06/ bridges06.html.
[4] Colin C. Adams, The Knot Book, The American Mathematical Society, Providence, RI, 2004.

Copyright and Reproduction of the Figures

All figures in the Encyclopedia are copyrighted by Robert Fathauer. Please request permission to reproduce any of the figures for any purpose.

Go to Compendium Home

Webmaster: Robert Fathauer; tessella@futureone.com