
Profiles in Math & Art
There are many notable figures in history that have done work that bridges the disciplines of mathematics and art. Some were professional artists and some scientists or mathematicians. The small sampling here is arranged in chronological order.

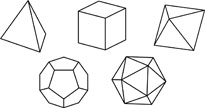 Plato (427-348 B.C.)
Greek philosopher, wrote about the five regular solids commonly known as the "Platonic solids". However, they predate him, and details concerning the original discovery of these polyhedra are not known. Plato related these solids to the basic elements, with fire assigned to the tetrahedron, air to the octahedron, water to the icosahedron, and earth to the cube. Plato further wrote "There was yet a fifth combination which God used in the delineation of the Universe" (Timaeus, 55d-e), namely the dodecahedron.
Plato (427-348 B.C.)
Greek philosopher, wrote about the five regular solids commonly known as the "Platonic solids". However, they predate him, and details concerning the original discovery of these polyhedra are not known. Plato related these solids to the basic elements, with fire assigned to the tetrahedron, air to the octahedron, water to the icosahedron, and earth to the cube. Plato further wrote "There was yet a fifth combination which God used in the delineation of the Universe" (Timaeus, 55d-e), namely the dodecahedron.
"The knowledge of which geometry aims is the knowledge of the eternal."
To browse products related to the Platonic solids, click here.

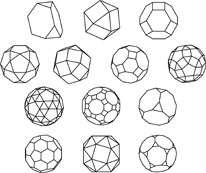 Archimedes (c 290/280 - 212/211 B.C.)
The most famous mathematician and scientist of ancient Greece. He discovered the relation between the surface and volume of a sphere. He also described the 13 semi-regular polyhedra; i.e., those made up of two regular polygons for which each vertex is of the same type. Just as the regular polyhedra are referred to as the Platonic solids, the semi-regular polyhedra are commonly referred to as the Archimedean solids. His writings on them were lost, together with the figures. They were gradually rediscovered during the Renaissance, and all 13 did not appear together until Johannes Kepler's Harmonices Mundi was published in 1619, nearly two millennia after Archimedes' death! There are 11 plane tilings made of up of regular polygons for which each vertex is of the same type, and these are referred to as the Archimedean tilings. Three of these are regular (those by equilateral triangles, squares, and hexagons), and 8 are semi-regular. Archimedes was a man who truly loved mathematics. Plutarch (c 46-127) wrote of him: "... being perpetually charmed by his familiar siren, that is, by his geometry, he neglected to eat and drink and took no care of his person; that he was often carried by force to the baths, and when there he would trace geometrical figures in the ashes of the fire, and with his finger draw lines upon his
body when it was anointed with oil, being in a state of great ecstasy and divinely possessed by his science."
Archimedes (c 290/280 - 212/211 B.C.)
The most famous mathematician and scientist of ancient Greece. He discovered the relation between the surface and volume of a sphere. He also described the 13 semi-regular polyhedra; i.e., those made up of two regular polygons for which each vertex is of the same type. Just as the regular polyhedra are referred to as the Platonic solids, the semi-regular polyhedra are commonly referred to as the Archimedean solids. His writings on them were lost, together with the figures. They were gradually rediscovered during the Renaissance, and all 13 did not appear together until Johannes Kepler's Harmonices Mundi was published in 1619, nearly two millennia after Archimedes' death! There are 11 plane tilings made of up of regular polygons for which each vertex is of the same type, and these are referred to as the Archimedean tilings. Three of these are regular (those by equilateral triangles, squares, and hexagons), and 8 are semi-regular. Archimedes was a man who truly loved mathematics. Plutarch (c 46-127) wrote of him: "... being perpetually charmed by his familiar siren, that is, by his geometry, he neglected to eat and drink and took no care of his person; that he was often carried by force to the baths, and when there he would trace geometrical figures in the ashes of the fire, and with his finger draw lines upon his
body when it was anointed with oil, being in a state of great ecstasy and divinely possessed by his science."
To browse products related to the Archimedean solids, click here.

 Leonardo da Vinci (1452-1519)
Leonardo da Vinci is famous for his accomplishments both as an inventor and as an artist. His notebooks contain the first known examples of the anamorphic art . These "slant anamorphoses" present objects which must be viewed at an angle to appear undistorted. He also made numerous drawings of symmetric knot designs. In addition, his illustrations of polyhedra in the 1509 book "De Divina Proportione", by Luca Pacioli are the first example of the use of frames that show the backsides the polyhedra as well as their frontsides.
Leonardo da Vinci (1452-1519)
Leonardo da Vinci is famous for his accomplishments both as an inventor and as an artist. His notebooks contain the first known examples of the anamorphic art . These "slant anamorphoses" present objects which must be viewed at an angle to appear undistorted. He also made numerous drawings of symmetric knot designs. In addition, his illustrations of polyhedra in the 1509 book "De Divina Proportione", by Luca Pacioli are the first example of the use of frames that show the backsides the polyhedra as well as their frontsides.
"Mechanics is the paradise of the mathematical sciences, because by means of it one comes to the fruits of mathematics."
For T-shirts featuring Leonardo's polyhedra, click here.

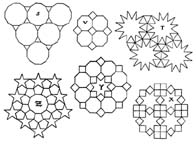 Johannes Kepler (1580-1630)
Well known for his work in astronomy, Kepler also had a keen interest in geometric tessellations and polyhedra . In his book Harmonice Mundi (1619), he published a number of tilings of regular and star polygons.
Johannes Kepler (1580-1630)
Well known for his work in astronomy, Kepler also had a keen interest in geometric tessellations and polyhedra . In his book Harmonice Mundi (1619), he published a number of tilings of regular and star polygons.
"The chief aim of all investigations of the external world should be to discover the rational order and harmony which has been imposed on it by God and which He revealed to us in the language of mathematics."
For tessellation sets with regular and star polyhedra, click here.
 Johann Sebastian Bach (1685-1750)
Mathartfun.com is primarily concerned with the visual arts, but math and music can be combined as well, of course. In fact, music has strong inherent mathematical content in both the meter and the tonal spacings. Bach, however, went beyond these to create a variety of compositions that are especially pleasing to those with a mathematical inclination. His fugues and cannons are particularly mathematical in nature. Bach also played clever games with music. For example, a sheet of music with his "Crab Cannon" on it can literally be turned upside down and remain unchanged. Escher had a special affinity for Bach, which he wrote about on more than one occasion. "In my periods of weakness and spiritual emptiness and lethargy, I reach out to Bach's music to revive and fire my desire for creativity."
Johann Sebastian Bach (1685-1750)
Mathartfun.com is primarily concerned with the visual arts, but math and music can be combined as well, of course. In fact, music has strong inherent mathematical content in both the meter and the tonal spacings. Bach, however, went beyond these to create a variety of compositions that are especially pleasing to those with a mathematical inclination. His fugues and cannons are particularly mathematical in nature. Bach also played clever games with music. For example, a sheet of music with his "Crab Cannon" on it can literally be turned upside down and remain unchanged. Escher had a special affinity for Bach, which he wrote about on more than one occasion. "In my periods of weakness and spiritual emptiness and lethargy, I reach out to Bach's music to revive and fire my desire for creativity."
 Sir David Brewster (1781-1868)
Scottish physicist noted for his experimental work in optics and polarized light. He was trained as a minister, but his fear of public speaking and his interest in science caused his life to take a different turn. Brewster invented the kaleidoscope in 1816. He was elected a fellow of the Royal Sociey in 1815 and knighted in 1831.
Sir David Brewster (1781-1868)
Scottish physicist noted for his experimental work in optics and polarized light. He was trained as a minister, but his fear of public speaking and his interest in science caused his life to take a different turn. Brewster invented the kaleidoscope in 1816. He was elected a fellow of the Royal Sociey in 1815 and knighted in 1831.

 Koloman Moser (1868-1918)
Graphic artist who taught in Vienna and worked in the Art Nouveau style. He executed a couple of tessellations around 1899-1900 that are remarkably Escheresque in style, though Escher was apparently not aware of Moser's work until 1964.
Koloman Moser (1868-1918)
Graphic artist who taught in Vienna and worked in the Art Nouveau style. He executed a couple of tessellations around 1899-1900 that are remarkably Escheresque in style, though Escher was apparently not aware of Moser's work until 1964.

 Piet Mondrian (1872-1944)
Dutch painter known for his geometric abstractions; several of his paintings depict rectangular blocks of color separated by black lines.
Piet Mondrian (1872-1944)
Dutch painter known for his geometric abstractions; several of his paintings depict rectangular blocks of color separated by black lines.
"The proportions and rhythm of planes and lines in architecture will mean more to the artist than the capriciousness of nature. In the metropolis, beauty expresses itself more mathematically; therefore it is the place out of which the mathematically artistic temperatment of the future must develop, the place out of which the New Style must emerge."

 R. Buckminster Fuller (1895-1983)
R. Buckminster Fuller was an architect, engineer, and more who had a keen interest in design and technology. He is best known for his geodesic domes. He was also a futurist with often unconventional views on global issues. His designs of a range of objects, including automobiles and houses, drew considerable attention in his day.
R. Buckminster Fuller (1895-1983)
R. Buckminster Fuller was an architect, engineer, and more who had a keen interest in design and technology. He is best known for his geodesic domes. He was also a futurist with often unconventional views on global issues. His designs of a range of objects, including automobiles and houses, drew considerable attention in his day.
 M.C. Escher (1898-1972)
Maurits Cornelis Escher was born in Leeuwarden, Holland. He was not very good at mathematics in school, and was a graphic artist by training and profession. Early in his career, he spent much of his time in Italy, where he made a number of more-or-less traditional woodcuts. After a trip to the Alhambra, in Granada, Spain, Escher became fascinated with tessellations. It was at this time, in the 1930's, that his work began to turn away from traditional subjects to mathematical and fanciful ones. Starting around 1950, he began to receive international acclaim. His work was never really accepted by the art establishment, but was embraced enthusiastically by mathematicians and scientists. His work covered a range of topics, including tessellations, Moebius strips, impossible figures, polyhedra, and unusual takes on perspective drawing. While Escher's primary goal in many of his prints is the exposition of a mathematical idea, his work also deals with philosophical issues, most notably the infinite, dualities such as heaven and hell, and man's mortality.
M.C. Escher (1898-1972)
Maurits Cornelis Escher was born in Leeuwarden, Holland. He was not very good at mathematics in school, and was a graphic artist by training and profession. Early in his career, he spent much of his time in Italy, where he made a number of more-or-less traditional woodcuts. After a trip to the Alhambra, in Granada, Spain, Escher became fascinated with tessellations. It was at this time, in the 1930's, that his work began to turn away from traditional subjects to mathematical and fanciful ones. Starting around 1950, he began to receive international acclaim. His work was never really accepted by the art establishment, but was embraced enthusiastically by mathematicians and scientists. His work covered a range of topics, including tessellations, Moebius strips, impossible figures, polyhedra, and unusual takes on perspective drawing. While Escher's primary goal in many of his prints is the exposition of a mathematical idea, his work also deals with philosophical issues, most notably the infinite, dualities such as heaven and hell, and man's mortality.
"In mathematical quarters, the regular division of the plane has been considered theoretically, since it forms part of crystallography. Does this mean that it is an exclusively mathematical question? In my opinion, it does not. Crystallographers . . . have opened the gate to an extensive domain, but they have not entered this domain themselves. By their very nature, they are more interested in the way in which the gate is opened than in the garden lying behind it."
For neckties based on Escher's art, click here.

 Salvador Dali (1904-1989)
Flamboyant and controversial Spanish surrealist painter who employed mathematics in some of his work. His "Crucifixion" of 1954 depicts a hypercube, and his "La Visage de la Guerre" of 1940 depicts a fractal progression of ever smaller death masks. He also executed a set of erotic anamorphic paintings.
Salvador Dali (1904-1989)
Flamboyant and controversial Spanish surrealist painter who employed mathematics in some of his work. His "Crucifixion" of 1954 depicts a hypercube, and his "La Visage de la Guerre" of 1940 depicts a fractal progression of ever smaller death masks. He also executed a set of erotic anamorphic paintings.
 Max Bill (1908-1994)
Max Bill was a graphic artist, sculptor, and painter who studied at the Bauhaus. He made a number of sculptures based Moebius strips, many of which are displayed in public places.
Max Bill (1908-1994)
Max Bill was a graphic artist, sculptor, and painter who studied at the Bauhaus. He made a number of sculptures based Moebius strips, many of which are displayed in public places.
"I am convinced it is possible to evolve a new form of art in which the artist's work could be founded to quite a substantial degree on a mathematical line of approach to its content."
 Victor Vasarely (1906-1997)
Hungarian-born painter known as the leading pioneer and practitioner of optical art ("op art"). He studied at the Bauhaus in Budapest and in 1930 moved to Paris where he developed his distinctive style. He uses the coloring of simple geometric shapes, often in arrays, to suggest motion and concave/convex effects on a flat canvas.
Victor Vasarely (1906-1997)
Hungarian-born painter known as the leading pioneer and practitioner of optical art ("op art"). He studied at the Bauhaus in Budapest and in 1930 moved to Paris where he developed his distinctive style. He uses the coloring of simple geometric shapes, often in arrays, to suggest motion and concave/convex effects on a flat canvas.

 Benoit Mandelbrot (1924-2010)
Mathematician who was largely responsible for formalizing and popularizing the concept of fractals. He discovered the Mandelbrot set, the best-known of fractal objects. He also coined the term "fractal", derived from the Latin word "fractus", meaning fragmented or broken.
Benoit Mandelbrot (1924-2010)
Mathematician who was largely responsible for formalizing and popularizing the concept of fractals. He discovered the Mandelbrot set, the best-known of fractal objects. He also coined the term "fractal", derived from the Latin word "fractus", meaning fragmented or broken.
"Can pure geometry be perceived by the 'man in the street' as beautiful? To be more specific, can a shape that is defined by a simple equation or a simple rule of construction be perceived by people other than geometers as having aesthetic value - namely, as being at least surprisingly decorative - or prehaps even as being a work of art? When the geometric shape is a fractal, the answer is yes."
For books and other products related to fractals, click here.

 Charles Perry (1929-2011)
Architect and sculptor who created a number of large mathematical sculptures for public places. Many of his pieces are based on topological constructs related to Möbius strips and knots.
Charles Perry (1929-2011)
Architect and sculptor who created a number of large mathematical sculptures for public places. Many of his pieces are based on topological constructs related to Möbius strips and knots.
"Somehow the structures of shells, leaves, bubbles and bones ... had far more natural beauty to me than did the sculpted bronze buttocks of a horse."
Math + Art topics
mathartfun.com home
© 2000-2015 Tessellations

 Plato (427-348 B.C.)
Greek philosopher, wrote about the five regular solids commonly known as the "Platonic solids". However, they predate him, and details concerning the original discovery of these polyhedra are not known. Plato related these solids to the basic elements, with fire assigned to the tetrahedron, air to the octahedron, water to the icosahedron, and earth to the cube. Plato further wrote "There was yet a fifth combination which God used in the delineation of the Universe" (Timaeus, 55d-e), namely the dodecahedron.
Plato (427-348 B.C.)
Greek philosopher, wrote about the five regular solids commonly known as the "Platonic solids". However, they predate him, and details concerning the original discovery of these polyhedra are not known. Plato related these solids to the basic elements, with fire assigned to the tetrahedron, air to the octahedron, water to the icosahedron, and earth to the cube. Plato further wrote "There was yet a fifth combination which God used in the delineation of the Universe" (Timaeus, 55d-e), namely the dodecahedron. Archimedes (c 290/280 - 212/211 B.C.)
The most famous mathematician and scientist of ancient Greece. He discovered the relation between the surface and volume of a sphere. He also described the 13 semi-regular polyhedra; i.e., those made up of two regular polygons for which each vertex is of the same type. Just as the regular polyhedra are referred to as the Platonic solids, the semi-regular polyhedra are commonly referred to as the Archimedean solids. His writings on them were lost, together with the figures. They were gradually rediscovered during the Renaissance, and all 13 did not appear together until Johannes Kepler's Harmonices Mundi was published in 1619, nearly two millennia after Archimedes' death! There are 11 plane tilings made of up of regular polygons for which each vertex is of the same type, and these are referred to as the Archimedean tilings. Three of these are regular (those by equilateral triangles, squares, and hexagons), and 8 are semi-regular. Archimedes was a man who truly loved mathematics. Plutarch (c 46-127) wrote of him: "... being perpetually charmed by his familiar siren, that is, by his geometry, he neglected to eat and drink and took no care of his person; that he was often carried by force to the baths, and when there he would trace geometrical figures in the ashes of the fire, and with his finger draw lines upon his
body when it was anointed with oil, being in a state of great ecstasy and divinely possessed by his science."
Archimedes (c 290/280 - 212/211 B.C.)
The most famous mathematician and scientist of ancient Greece. He discovered the relation between the surface and volume of a sphere. He also described the 13 semi-regular polyhedra; i.e., those made up of two regular polygons for which each vertex is of the same type. Just as the regular polyhedra are referred to as the Platonic solids, the semi-regular polyhedra are commonly referred to as the Archimedean solids. His writings on them were lost, together with the figures. They were gradually rediscovered during the Renaissance, and all 13 did not appear together until Johannes Kepler's Harmonices Mundi was published in 1619, nearly two millennia after Archimedes' death! There are 11 plane tilings made of up of regular polygons for which each vertex is of the same type, and these are referred to as the Archimedean tilings. Three of these are regular (those by equilateral triangles, squares, and hexagons), and 8 are semi-regular. Archimedes was a man who truly loved mathematics. Plutarch (c 46-127) wrote of him: "... being perpetually charmed by his familiar siren, that is, by his geometry, he neglected to eat and drink and took no care of his person; that he was often carried by force to the baths, and when there he would trace geometrical figures in the ashes of the fire, and with his finger draw lines upon his
body when it was anointed with oil, being in a state of great ecstasy and divinely possessed by his science."  Leonardo da Vinci (1452-1519)
Leonardo da Vinci is famous for his accomplishments both as an inventor and as an artist. His notebooks contain the first known examples of the anamorphic art . These "slant anamorphoses" present objects which must be viewed at an angle to appear undistorted. He also made numerous drawings of symmetric knot designs. In addition, his illustrations of polyhedra in the 1509 book "De Divina Proportione", by Luca Pacioli are the first example of the use of frames that show the backsides the polyhedra as well as their frontsides.
Leonardo da Vinci (1452-1519)
Leonardo da Vinci is famous for his accomplishments both as an inventor and as an artist. His notebooks contain the first known examples of the anamorphic art . These "slant anamorphoses" present objects which must be viewed at an angle to appear undistorted. He also made numerous drawings of symmetric knot designs. In addition, his illustrations of polyhedra in the 1509 book "De Divina Proportione", by Luca Pacioli are the first example of the use of frames that show the backsides the polyhedra as well as their frontsides.
 Charles Perry (1929-2011)
Architect and sculptor who created a number of large mathematical sculptures for public places. Many of his pieces are based on topological constructs related to Möbius strips and knots.
Charles Perry (1929-2011)
Architect and sculptor who created a number of large mathematical sculptures for public places. Many of his pieces are based on topological constructs related to Möbius strips and knots.