
Dendritic Fractal Tiles that Admit Monohedral Tilings

Procedure for generating these types of tiles:
1) Start with a simple periodic tessellation, with colored tiles and white "tiles" representing gaps. The particular colored grids used here are convenient starting points, but there are other possibilities.
2) Identify a small unit cell with corners located at the centers of white spaces. Then identify a larger unit cell of the same shape, but in most cases a different orientation.
3) Fill in the white spaces in the larger unit cell, except for the corner spaces, in a manner that produces a tile that will tessellate except for the corner spaces.
4) Create the same tile in a second color, usually rotated with respect to the first tile. Tessellate a large enough area with the tiles to allow further iterations.
5) Fill in white spaces in this new tiling in an analogous manner to that used to fill white spaces in the starting grid.
6) Iterate as many times as desired, being careful to be consistent.
In the limit, the area occupied by white gaps goes to zero, leaving a two-color tiling of fractal tiles. For a dendritic tile that is not fractal, a tessellating tile can be formed at any stage by adding triangles at open spaces, as shown here.
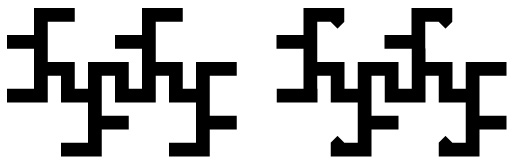

This starts out the same as the twindragon example above, but a different choice is made for joining tiles starting in the fourth iteration.
In this example, 4/5 of the untiled spaces are filled with each iteration. The tiles have four-fold symmetry. Below the video a single tile is shown after an additional iteration.

With each iteration, 2/3 of the untiled hexagonal spaces are filled. The center of each white hexagon is a point of six-fold rotational symmetry, ignoring coloring. The tiles have three-fold symmetry. Below the video a single tile is shown after an additional iteration. Van Deventer produced a fractal jigsaw puzzle based on such tiles.

With each iteration, 6/7 of the untiled hexagonal spaces are filled. Each white hexagon is a point of six-fold rotational symmetry, ignoring coloring. The tiles have three-fold symmetry. A second tile is colored green in the last frame to elucidate how the tiles fit together. Below the video a single tile is shown after an additional iteration.

A related tile that tessellates at each iteration can be obtained by iterating a simple "I" tessellation. With each iteration another leg is added to each spiral. The number of squares comprising each tile scales as 9, 25, 49, 81, etc.

All images copyright Robert Fathauer
Robert Fathauer's Fractal Diversions home
Fractal Tiling
 Fractal Knots
Fractal Knots
 Gasket Fractals
Gasket Fractals
 Fractal Trees
Fractal Trees
 Hyperbolic & Folded Fractals
Hyperbolic & Folded Fractals
 Polyhedra
Polyhedra
 Papers etc.
Papers etc.