
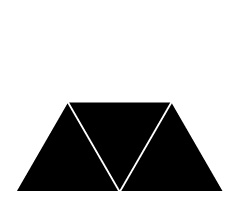
Equilateral triangle divided by four

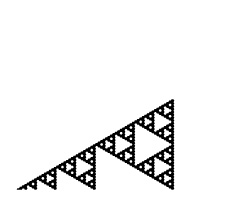
The scaling factor from one generation to the next is 0.5. This is the template for the Sierpinski Triangle, also known as the Sierpinski Gasket, shown at far left below. This reptile has three-fold rotational symmetry and mirror symmetry, allowing for choices in the orientation of the smaller units in cases where those units have less symmetry than an equilateral triangle.
If overall rotations or reflections are not considered distinct, there are two possibilities for removing one triangle in the first iteration. One is removal of the center triangle, and the other is removal of a corner triangle. For the center triangle, the iteration rules are fully defined, and the only possibility is the Sierpinski Triangle. For the corner triangle, there are 27 possibilities for the second iteration, 15 of which are distinct. Of these, 3 have mirror symmetry and therefore a single possibility for a third iteration, while 12 lack mirror symmetry and therefore have 8 possibilities for a third iteration. The construction rules are fully locked in after three iterations, making the total number of distinct fractals 1 + 3 + 12*8 = 100. Three of these are shown below through eight iterations, along with the Sierpinski Triangle. The ninth iteration of the gasket at far right is shown at a larger scale at the bottom of the page. Fractal gaskets made using this reptile are discussed on Larry Riddle's page
"Triangle Fractals", and all 99 of the non-Sierpinski fractals are show on his page "Gallery of Triangle Fractals".





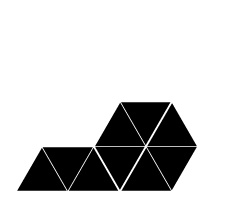
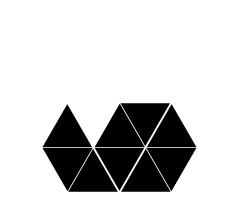










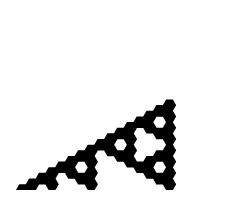




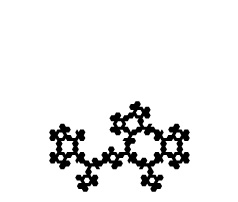


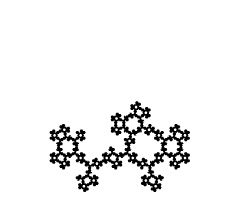


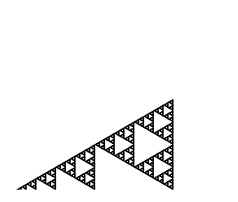
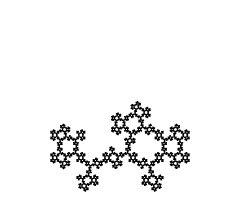
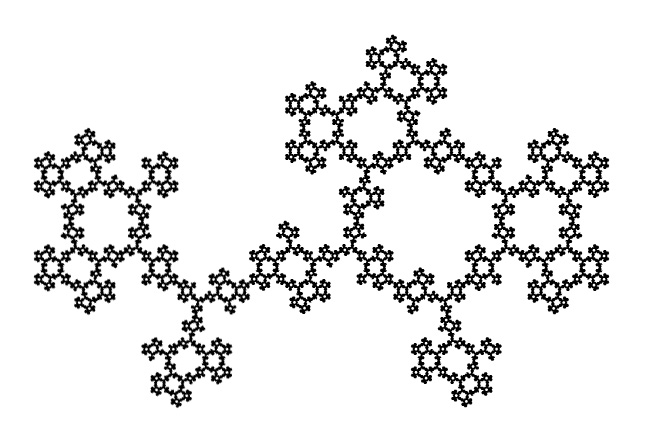
A spatially-developing fractal-gasket polyhedron based on a gasket that is similar to the right one above, with the top layer colored black:
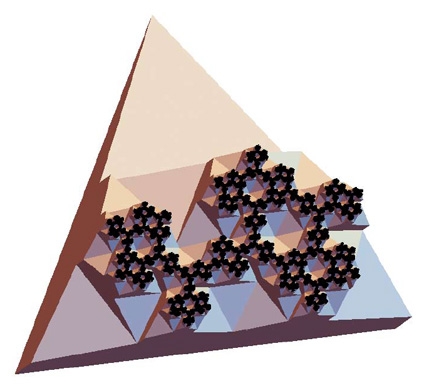
All images copyright Robert Fathauer
Fractal Diversions home
Fractal Tiling
 Fractal Knots
Fractal Knots
 Gasket Fractals
Gasket Fractals
 Fractal Trees
Fractal Trees
 Hyperbolic & Folded Fractals
Hyperbolic & Folded Fractals
 Polyhedra
Polyhedra
 Papers
Papers