Walkable Curves

Hilbert Curve

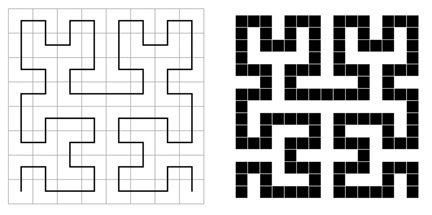
Fractal curves provide convenient templates for walkable mathematical structures. The Hilbert curve is particularly easy to work with due to the face that it is based on a square grid. The curve is basically an algorithm for connecting the squares in a grid to form a non-intersecting path. This is illustrated at left in the following figure. The curve is covered with smaller squares at right that define a path equal in width to the spacing between the rows of squares. If each of these squares is imagined to be a stepping stone, a walkable tower can be constructed. A version that can be manipulated in 3D is below.

Gosper Curve

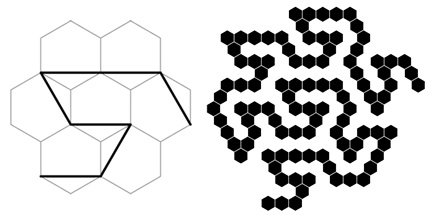
The Gosper curve is a plane-filling curve that provides an algorithm for connecting a tiling of hexagons, as shown at left here. It can be covered with hexagons in a similar manner to that used for the Hilbert curve with squares. This results in a chain of hexagons, a polyhex, with gaps that are long chains of hexagons, as shown at right for the second iteration of the curve. If the hexagons are treated as stepping stones, the tower-like structure below results.

Sierpinski Carpet Curve

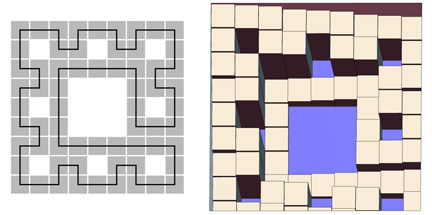
A third example is based on a path I discovered a few years ago that connects the squares comprising a Sierpinski Carpet, shown at left here. The large open square in the center of this curve brought stepwells to mind. Making each square in the curve a square step results in the structure at right. These sorts of broad square steps do not evoke actual stepwells very strongly, so I decided to add small flights of stairs between the large squares, which become landings, as shown below.

All images copyright Robert Fathauer

Robert Fathauer's Fractal Diversions home

Fractal Tiling Fractal Knots Gasket Fractals Fractal Trees Hyperbolic & Folded Fractals Polyhedra Papers etc.