Method for Creating Fractal Reptiles Based on Polyforms

A self-replicating tile, or reptile, is a tile that can be tiled by smaller copies of itself, as well as tiling the plane. The simplest example is a square, which can be tiled by four smaller squares. Denote by n the smallest number of smaller tiles a reptile can be divided into. The linear scaling factor is then √n. For a square, n = 4. A square can also be divided into 9 smaller squares, 16, etc., but 4 is the smallest possible number.

When fractals were identified as a distinct branch of geometry, it was recognized early on that fractal reptiles could be formed by iteration. In The Fractal Geometry of Nature, Mandelbrot shows three examples based on iterating curves to form four-fold polyominoes. Bandt pointed out that reptiles can be constructed from any map that transforms the lattice of integer vectors to itself [Proc. American Mathematical Society, vol. 112, 1991, pp. 549-563).

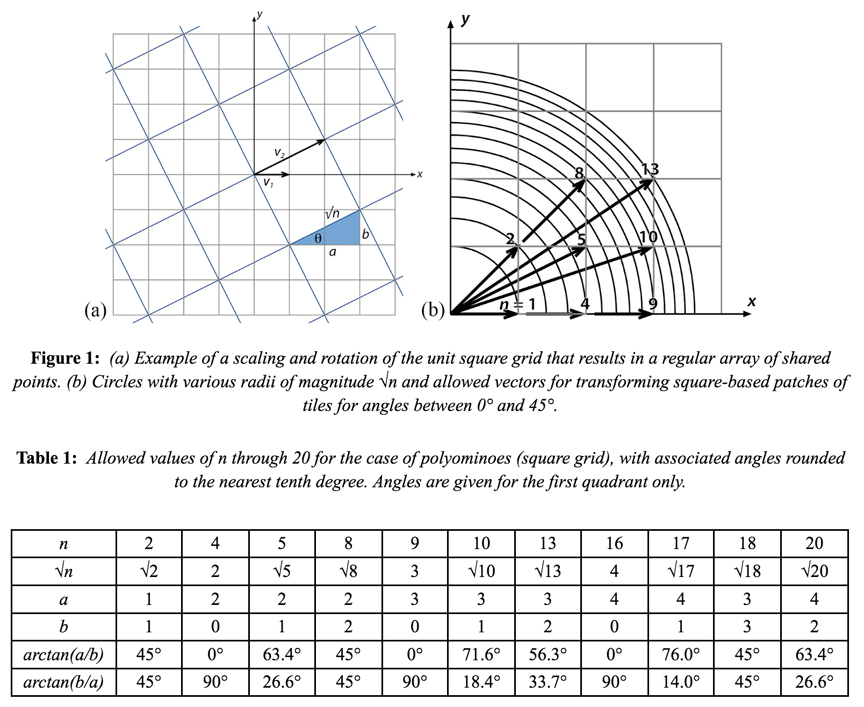
This site use a graphical approach to creating a variety of fractal forms, with an emphasis on the most interesting and beautiful examples. Polyforms provide a convenient selection of starting shapes. Allowed transformations can be identified by examining square and triangular grids, the latter including the hexagon case, as regular hexagons can be divided into six equilateral triangles. Figure 1 and Table 1 show the possible transformations consisting of scaling and rotation for polyominoes through order 20.

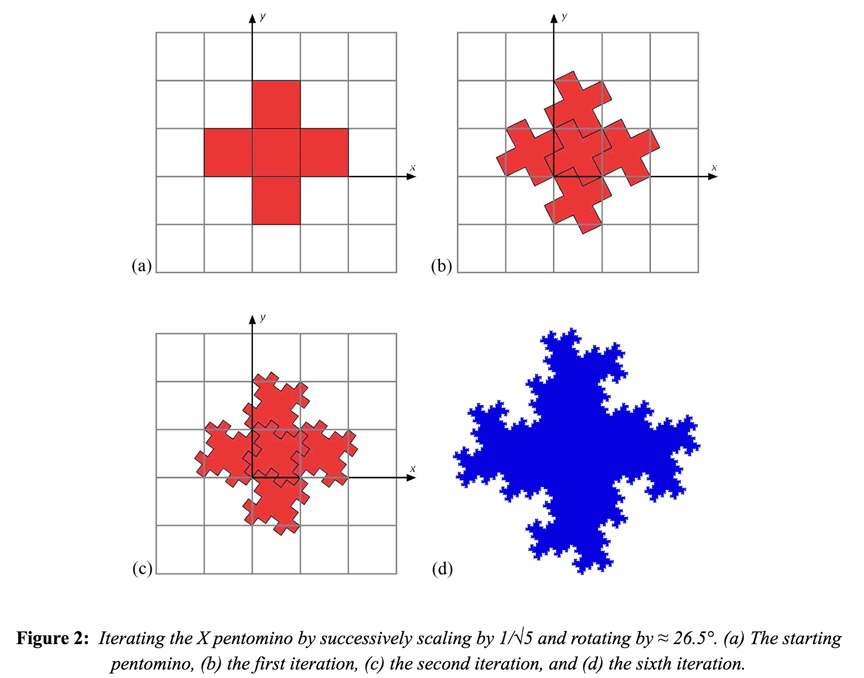
The method is illustrated in Figure 2 for the case of the X pentomino. Starting with a square with lower left corner at the origin, the pentomino is generated by translating copies one unit in each of four directions. With n = 5 there is an allowed rotation angle of approximately 26.6°. Rotating the starting polyomino by that amount about the origin and scaling by √5 results in a smaller X with vertices that coincide with those of the starting square. Scaling and translating four copies of this by one unit in each of four directions yields the patch of Figure 2(b). After another iteration, Figure 2(c) is obtained, with Figure 2(d) showing the tile after six iterations. At this scale, it is essentially indistinguishable from the fractal reptile that would be obtained after an infinite number of iterations. The fractal tile tessellates the plane and can be subdivided into five smaller copies of itself.

As noted previously using other construction methods, mirroring between iterations can result in different fractal reptiles [4]. Note that rotating and then mirroring is equivalent to mirroring alone by a different angle. For example, the transformed grid in Figure 1(a), obtained by rotating by arctan(b/a) could also be obtained by mirroring about a line at half that angle.

Codifying the construction steps:
1. Select a starting polyomino, consisting of n squares, that tiles the plane by translation. Placing a single square at the origin, build the polyomino by a combination of translations and/or reflections of copies of that starting square.
2. Scale by 1/√n about the origin and either rotate or reflect the polyomino according to allowed angles from Table 1. Form the first iteration by arranging n copies of the polyform in identical fashion to that by which the polyomino was built.
3. If the first iteration also tiles, additional iterations may be performed in the same manner. I.e., repeat step 2 as many times as desired using the current iteration. In general, while the tile will tessellate at every stage, it will only be self replicating in the limit of an infinite number of iterations.

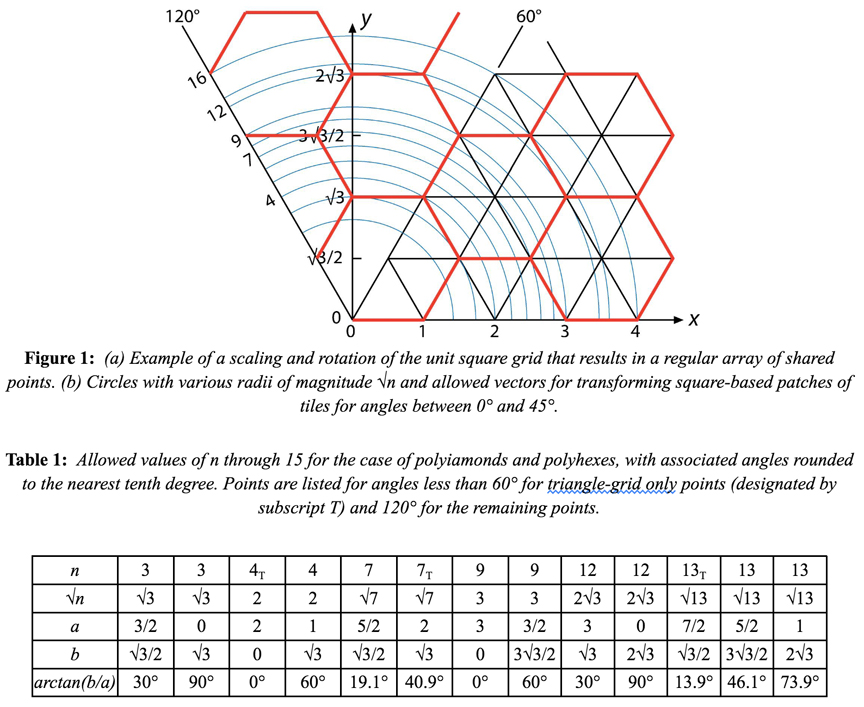
Figure 3 and Table 2 show possibilities for polyiamonds and polyhexes through order 15.